The Four-Color Theorem

The Four-Color Theorem

Normally, when you color in a pattern in a coloring book, you don’t pay attention to how many colors you need. You use as many crayons as you have available. But, what if you only had two or three or four crayons and you were asked not to let any color meet the same color at any edge, could you do it?

Let’s see.

Materials:

• 4 colors of crayons or colored pencils or pens
• Paper
• Straight edge
• Optional: Blank U.S. map

Instructions:

• Draw a grid that is 3×3, that is a square, divided into 9 squares in 3 rows and 3 columns
• Color the squares of the grid in such a way that the edges of the squares do not have the same color on the edge of the next square. It’s ok for corners to meet that are the same color, just not the edges of the squares.
• What is the smallest number of colors you need to make sure no two edges have the same color in the side-by-side squares?

What Should Happen?

You can color nine squares in alternating colors without having any two edges the same color with only two crayons.

This can be accomplished if your 3×3 grid looks like this:

• 1^st row: Yellow square – red square – yellow square
• 2^nd row: Red square – yellow square – red square
• 3^rd row: Yellow square – red square – yellow square

Let’s try another one.

Draw one circle inside another. Then, divide the outer ring into four even pieces. Now, how many colors do you need, with the same instructions, no edges that meet have the same color.

What Should Happen?

You can do it with three colors.

The colored circles will look like this:

• The center circle will be one color
• The four sections around the circle will alternate two other colors.

Optional:

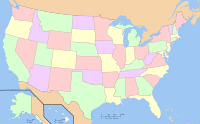
Color in the blank map of the United States. What is the fewest number of colors you can use without any edges meeting that are the same color?

What Should Happen?

The answer is, you only need four colors.

On October 23, 1852, Francis Guthrie, then a university student, later a professor of mathematics, on coloring in counties in England noticed that he only needed four colors to make the maps. He asked his professor if this was always true. It wasn’t until 1976 that mathematicians Kenneth Apel and Wolfgang Haken at the University of Illinois proved that it was true no matter what the map looked like.

They announced their proof on June 21, 1976, a problem that had taken nearly 124 years to prove, and one that became the first theorem proved with a computer. The math department at the University of Illinois began using a postmark, four colors suffice, that is, four colors are enough to color in a map of contiguous edges without edges of the same color meeting.

Why Is This Useful?

The 4-color theorem belongs to a branch of mathematics called topology. The maps are flat, not three-dimensional.

Topology is used for situations like figuring out the most efficient route for a school bus or truck to take to pick up and drop off students or deliver goods and in the design of computer networks.

Thank you to mathsisfun.com for this activity

Carol Covin, Granny-Guru

Author, “Who Gets to Name Grandma? The Wisdom of Mothers and Grandmothers”

http://newgrandmas.com

Don’t forget to follow Grandmother Diaries via Geek Girl on Facebook and Twitter.
Subscribe to updates by email

Filed in: arts & crafts & educational • education • Playtime Tags: four color theorem • four colors suffice